Craveology Cafe and the North Star Science Store are temporarily closed for renovation.

Orbits and Eccentricity
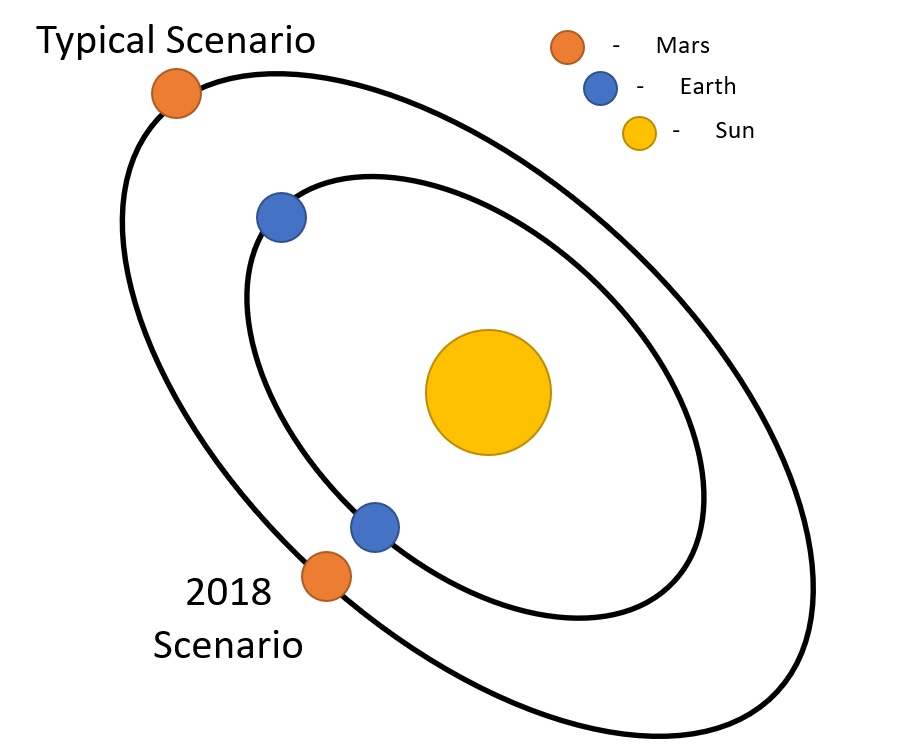
In 2018, during an event called Mars Opposition, Mars made its closest approach to Earth since 2003. This close approach will not happen again until 2035.
Because of the orbital periods of Mars and Earth, the planets make close approaches roughly once every two years. Why were the planets closer together in 2018 than in previous years?
Setup and Procedure
Ask: Does your drawing look circular or elliptical to your eye?
Ask: Can can we measure how much the drawing deviates from a perfect circle?
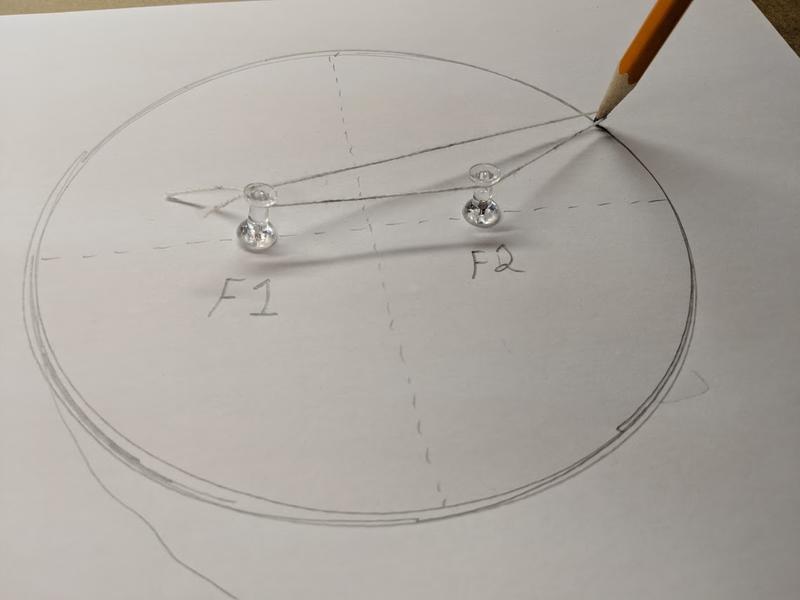
Add the following labels to your drawing so it can make these measurements:
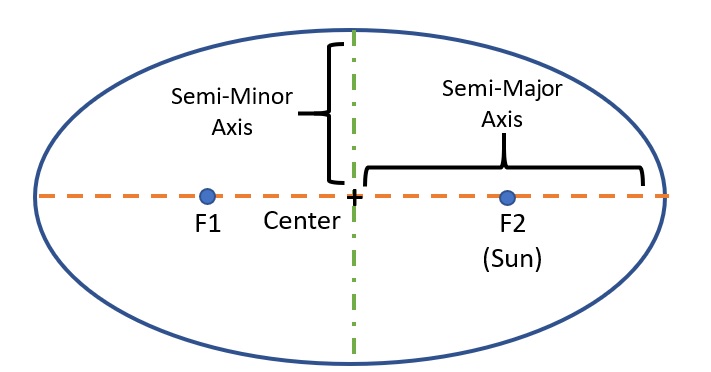
Additional Information: The “F” stands for “Focus.” Label one focus as “Sun.” It does not matter which focus is designated as the sun, but it is important to note that the sun is always at one of the foci. The second focus in our drawing is an empty point, but it’s location is measurable.
Eccentricity can be measured with the following formula:
|
E = 0
|
Circular Orbit
|
|
0 < E < 1 |
Elliptical Orbit
|
|
E = 1 |
Parabolic Trajectory
|
|
E > 1 |
Hyperbolic Trajectory
|
E = C/A
The value for E will vary depending on the length of string, the size of the loop created with the string and the distance between push-pins. However, with the materials outlined above, E should be between 0.1 and 0.3.
Flip over the sheet of paper and repeat the process above, except this time use one push-pin and trace your drawing using that one point. Follow all the steps, including labeling the drawing and placing measurements in the formula: E = C / A
Ask: By using one push-pin, E = 0. What questions do you have when E = 0?
Consider this: all orbits have two foci. When an orbit is a perfect circle, the foci overlap, giving the appearance of one focus. In our model, we represent this with one push-pin. By using one push-pin and a fixed length of string, the drawing is a perfect circle. The center-point between the foci and the distance between the center point and one of the focus is zero, so C = 0. If C = 0, then E = 0. When E = 0, there is no eccentricity. Any value over 0 indicates eccentricity, up to 0.9999.
|
PLANET |
ECCENTRICITY |
|
Mercury |
0.206 |
|
Venus |
0.007 |
|
Earth |
0.017 |
|
Mars |
0.093 |
|
Jupiter |
0.048 |
|
Saturn |
0.056 |
|
Uranus |
0.047 |
|
Neptune |
0.009 |
|
Pluto |
0.248 |
How does your model’s eccentricity match up with Solar System planet eccentricity? Compare your values for E with the chart to the right.
Assessment
Return to the initial question:
Based on your understanding of orbits, eccentricity and the planet data table above, draw a model that represents why in 2018 Mars made a close approach to Earth.
Models may look similar to to the figure below: